Happy New Year / Feliz Año Nuevo

Best wishes for New Year 2012.
Os deseo lo mejor para este nuevo año 2012.

Felices Fiestas / Feliz Navidad

Desearos a todos los lectores de NIR-Quimiometría unas Felices Fiestas, así como un Feliz Año 2012. Como otros años, yo soy uno más de las personas que se desplaza (por carretera) para pasar la Navidad con familiares, así que os quiero felicitar estas fiestas con esta foto tomada a pie de carretera entre Asturias y Madrid.

Spectroscopy Europe _T. Davies Column 06 -Dec -2011

Interesting article in Spectroscopy Europe :

Examining diffuse reflection and transmission spectra more thoroughly: Part 1. Instrument noise
by:
Karl H. Norris (Consultant, 11204 Montgomery Road, Beltsville, MD 20702, USA)
with
A.M.C. Davies (Norwich Near Infrared Consultancy, 10 Aspen Way, Cringleford, Norwich NR4 6UA, UK)

The December - 2011 issue of Tony Davies Column, were Karl H. Norris (considered the father of Near Infrared) writes a useful article to look more carefully at the spectra.
How we can use the 4th derivative to study the effect of noise in our data.

Next issue will continue with the second part.

Olive Paste: Calibration / Validation

I have developed an equation for olive paste, we can see the statistics of the database (number of samples, range, std. dev., mean), also the statistics of the equation, were the most importants are 1-VR  and SECV (cross validation statistics), also important the number of PLS factors, and the Math treatments for the model.

 This equations for fat and moisture has been added for routine analysis, and validated with a set of new samples of the new campaign 2011.

The validation statistics are:

Calibration performance is quite robust (not bias), and for the fat the Standard Error for Validation (SEP) is lower than the SECV of the calibration. For moisture is a little bit higher, but this is the normal case.

These samples and others, were added to the database and a new calibration developed. New equation statistics are almost similar to the old one. Anyway new variability has ben added of a new campaign and that is allways good.

If we want to improve SEP, we have to study if with some improvements in the sample presentation, replicates,....,improvement in the laboratory error,...,and so on, this statistic becomes lower, and at the same time the calibration stay robust.

IRIS Flower Data Set (R-003)

Centramos la matriz con el comando, generando a partir de A una nueva matriz que llamamos "Acentered"
Acentered=scale(A,center=T)
Ahora con la función "eigen":

Esta es otra forma de proceder con el cálculo de los componentes principales (eigenvectors y eigenvalues), como ya vimos en un post anterior.

IRIS Flower Data Set (R-002)

Ver  primero: IRIS Flower Data Set (R-001)

See first:        IRIS Flower Data Set (R-001)

El comando "summary" nos ayuda a comprender la importancia de cada componente principal:

Los "eigenvalues" son las desviaciones estándar al cuadrado:

Para comprobar la importancia de los eigenvalues, podemos verlos en forma de gráfico:

> lambda<-eigenvalues

> PCs<-c(1,2,3,4)

> plot(PCs,lambda)

save.image("H:\\BLOG\\Curso básico Quimiometria\\IRIS\\parte2.RData")

IRIS Flower Data Set (R-001)

IRIS Flower Data Set

Este es el Link a Wikipedia donde podéis encontrar los datos que utilizó Fisher en su trabajo de 1936. Ya hemos trabajado con estos datos en Excel y los continuaremos usando en nuevas entradas.

En este link, podemos ver las fotos de las flores (IRIS en castellano son lírios).

Represento como LS (longitud del sépalo), AS (anchura del sépalo), LP (longitud del pétalo), AP (anchura del pétalo).

Este es uno de los gráficos de Wikipedia:

Con estos datos ya hemos desarrollado algunos "posts", para familiarizarnos con el uso de matrices en Excel.

Vamos a usar estos mismos datos en fichero CSV e importarlos a "R" para trabajar con ellos, para ello usamos la función: read.table

Se muestran solo los 16 primeros datos por temas de espacio, pues en total son 150 (50 de cada clase).

Calculamos los componentes principales (centrados):

Representamos los "Mapas de Scores" con la función:
pairs(results2$x)
obteniendo:

save.image("H:\\BLOG\\Curso básico Quimiometria\\IRIS\\parte1.RData")

Tweet

Diagnostics: Water Vapour bands.

En ocasiones podemos ver en los espectros de ruido, bandas que destacan en la zona de absorción de la humedad (bandas de combinación en torno a 1940 nm y el primer sobretono en torno a 1450 nm), dicho sintoma nos indica que el equipo esta expuesto a una humedad ambiental alta. Es importante tomar medidas para reducir dicha humedad (debida a vapor de agua) y reducir las bandas hasta que sean lo menor posibles o que desaparezcan. Cuando queremos analizar constituyentes con muy baja concentración, la relación señal ruido del equipo debe de ser muy buena, y este tipo de espectros de ruido no contribuye a ello.
Sometimes we can see in the noise spectra, bands that stand in the absorption zone of moisture (combination bands around 1940 nm and the first overtone around 1450 nm), this symptom indicates that the equipment is exposed to a high humidity. It is important to take steps to reduce this moisture and reduce this water vapour bands until they are as small as possible or even disappear. When we analyze constituents with very low concentrations, the Signal to Noise Ratio of the instrument must be good, and this type of noise spectra does not contributes to this.

Tweet

Postcard from Antequera

Hacía tiempo que no ponía una postal en el Blog. Hoy me he animado a perderme por las calles de Antequera (Malaga) en busca de alguna postal para el blog y esta es la que más me ha gustado, porque transmite la tranquilidad de esta bonita ciudad en esta época del año.

Aprovecho el post para comentar algunas de las aplicaciones para que más se utiliza el NIR (Near Infrared Reflectance) en esta zona de Andalucia.

Por supuesto se trata aplicaciones relacionadas con su fruto más emblemático: "la aceituna". Las almazaras están a pleno rendimiento en esta campaña  y el NIR es una herramienta que predice la "humedad" y el "rendimiento graso" a la entrada del fruto (después de ser molida y de preparar una pasta) de una manera rápida y fiable. Se está trabajando también para obtener resultados aceptables para la acidez (en la pasta de aceituna), aunque se trata de un parámetro más complicado.

En el aceite se están analizando por NIT (Near Infrared Transmitance) parámetros como la acidez ( en este caso los resultados son buenos), peróxidos, Ks, humedad, ceras, eritrodiol + uvaol, acidos grasos,.....

Se esta trabajando también para obtener resultados adecuados para algunos de los parámetros importantes de la hoja de olivo (foliares).

Hablando de esta última opción hoy he leído en un artículo de un periódico local el gran potencial de propiedades para la salud (algunas de ellas anticancerígenas) de los extractos de hoja de olivo. Se trata de un estudio de la UCO (Universidad de Córdoba) publicado en la revista Mutation Research.

Pairs for the "P" (loadings) matrix

Ver primero: PCA file calculation with "R"

See first:         PCA file calculation with "R"

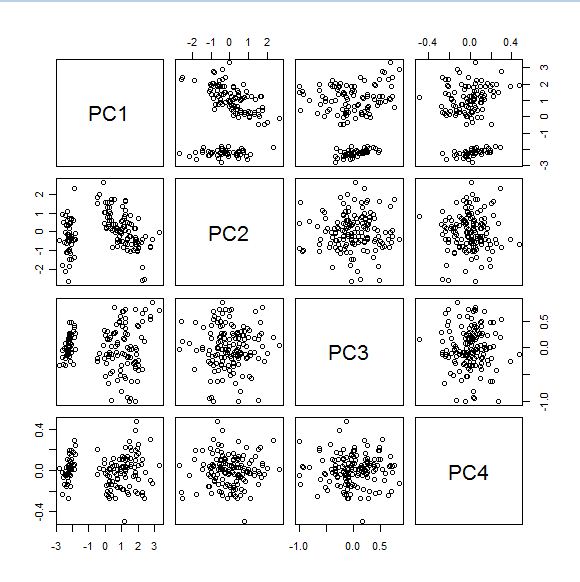
Podemos ver los diferentes planos que forman los PCs entre sí, con la función "Pairs" de "R".

We can see all the combinations of planes (which form the Principal Components) with the function  "Pairs" (R).

The Power of the Graphics

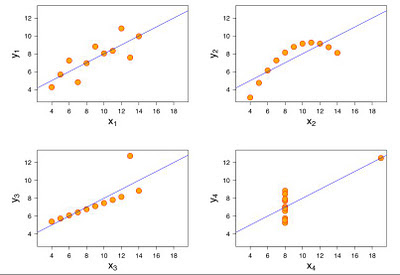
He visto en varias ocasiones (la última en: Data Mining and Predictive Analytics  ) este ejemplo (Anscombe's quartet), que nos sirve para entender la importancia de la visualización de los gráficos. El los cuatro casos las tablas de datos presentan la misma media, desviación estándar tanto para X como para Y, también la correlación X-Y es la misma en los cuatro casos. De modo que unicamente los datos estadísticos no serán suficientes para juzgar estos datos.

Adjunto las imágenes de Wikipedia.

I read not long ago an article in the Tony Davies Column about this (allways look at the plots), and in the last post of one of the blogs I follow (Data Mining and Predictive Analytics ) this matter comes again using this famous example (Anscombe's quartet) to understand the power of the graphics.

In the four figures, we have the same average,standard deviation, correlation,.., for "Y" and "X", so if somebody gives you only the numbers, your idea of how the graphics are can be wrong. You need to ask for the graphics, or to have the original data table to plot them.

I attach also the Wikipedia images.

Diagnostics: Warm-up Bias

Después de encendido el equipo (NIR), y encendida la lámpara no se deben de realizar análisis hasta que el equipo este estable. Una de las causas de esta inestabilidad inicial es el Bias, que al comienzo muestra variaciones muy grandes  hasta que el equipo se estabiliza en temperatura.

En la  imagen podemos ver  como el Bias (auto-escala) va disminuyendo en el tiempo (de arriba hacia abajo).
After turning on the computer (NIR), and the lamp,...analysis should not be  performed until the instrument is stable. One reason of this  initial unstability is the Bias, which at the beginning shows large variations until the instrument is stable in temperature.
In the picture we see how the Bias (auto-scale) decreases over time (from top to bottom).

El equipo estará estable una vez que los espectros de ruido esten entre +/- 0,100 (mAbs).
En la siguiente imagen, el Bias ya está en la escala adecuada y se ve como se distribuye de manera homogenea por el eje "0" y entre +/- 0,1 mAbs..
The instrument will be stable, once the noise spectra are between + / - 0.100 (mAbs).
In the next image, the bias is already at an appropriate scale (evenly distributed along the axis "0" and between +/- 0,100 mAbs).

Principal Components Analysis with "R" (Part: 001)

This is the first "post" of my new adventure with a software that I consider very interesting and that give to people the oportunity to work with Chemometrics ("R" is free).
To follow these examples, yo can download the following article:
"Multivariate Statistical Analysis using the R package chemometrics"

Decidimos seleccionar 5 CP, que explican casi el 80% de las varianza en este ejemplo.

We decided to select 5 PCs, which explain almost the 80% of the variance for this example.

Spectra Reconstruction (Excel / R)

Hemos visto estos calculos en muchas de las entrada de este blog.La parte azul esta desarrollada en "R", la negra en "Excel".

We have seen all these calculations in several posts. Blue part is calculated in "R", black part in Excel.

See posts:

PCA File calculation with "R".
Spectra recontruction.

PCA file calculation with "R".

X es la matriz centrada (X is the centered matrix).

Xcov es la matriz de covarianzas de X (Xcov is the covariance matrix of X).

Con la función "eigen" calculamos los "eigenvectors" y "eigenvalues" de Xcov.(With the function "eigen" we calculate the "eigenvectors" and "eigenvalues" of  Xcov).

Para hacer todo al mismo tiempo, podemos usar la función "prcomp".(To do everything at the same time we can use the function "prcomp").

La diferencia es que con eigen obtenemos la varianza y con prcomp las desviaciones estándar.

The diference is that with eigen we get the variances, and with prcomp the standard deviations.

Podemos comprobar estos resultados con el cálculo del fichero PCA de la entrada anterior.
We can compare this results with the PCA file got in Win ISI in the previous post.

Distancia de Mahalanobis_review 006

Ejemplo de distancia de Mahalanobis, con solo tres variables con los mismos datos (aportados por la Hoja Excel  de Pierre Dardenne en NIRS-Forum) desarrollados en Win ISI.

Mahalanobis Distance practice with only 3 variables (trying to understand the Excel file from Pierre Dardenne in NIRS-Forum)

Datos generados manualmente en Unscrambler, exportados a JCAM-DX e importados posteriormente a Win ISI.

Data generated manually in Unscrambler, exported to JCAM-DX and imported in Win ISI

CERTER.EXE

Se generan:

Fichero PCA

 

 Fichero LIB

Distancias de Mahalanobis al centro de la población

Mahalanobis distance to the mean

Continuará.
To be continued

Cross Validation Groups

La selección de número de grupos, así como el número de muestras que pertenecen a cada grupo, tiene cierta importancia a la hora de desarrollar nuestro modelo de calibración. Pongamos por ejemplo el caso de una calibración con 1000 muestras y creamos 2 grupos, por lo que 500 irán a un grupo y las otras 500 al otro. ¿Como lo hace?.

Se pueden seleccionar de una manera aleatoria.

Las pares a un grupo y las impares al otro.

Cuando se  crean mas grupos (3 por ejemplo) existen mas combinaciones para poder seleccionarlas:

La 1ª, 4ª, 7ª,......al primer grupo. La 2ª, 5ª, 8ª ,.....al segundo y la 3ª, 6ª, 9ª,..... al tercero

De manera aleatoria.

Cada tercio a un grupo.

....................................

Y no olvidemos la Full Cross Validation (leave one out) en la que hay tantos grupos como muestras.

Debemos de observar las opciones que tiene nuestro software para el desarrollo de la Cross Validation y seleccionar el que nos parezca más adecuado.

También debemos de tener en cuenta en función del que elijamos si ordenamos nuestro conjunto de calibración (en el caso de "leave one out" no tendría importancia) nuestras muestras por valor de constituyente, o por algún otro criterio como podría ser su distancia de Mahalanobis al centro de la población.

Lo recomendable es seguir algún tipo de orden y después seleccionar una selección de tipo sistemática, o seleccionar para los grupos las muestras de una manera aleatoria.

Debemos de tener en cuenta de que en el caso de que una "única muestra" sea muy especial en cierto momento formará parte del conjunto de validación y no habrá ninguna como ella en el de calibración, por lo que será detectada como anómala. Es por tanto conveniente que cuando una muestra esté en el grupo de validación existan muestras similares (en variedad, concentración de analito, procedencia,...,etc) en el conjunto de calibración.

Los estadísticos que obtengamos serán diferentes en función de los grupos, pero si la base de datos es lo suficiente robusta y la validación cruzada está bien estructurada, no debería de haber grandes diferencias.

Manera de selección de las muestras para validación cruzada en Unscrambler:

A History of the Sky

Otro interesante vídeo descubierto a través de:

http://blog.revolutionanalytics.com/

Realmente impresionante este vídeo en el que se muestra una fotograma del cielo, cada 10 segundos, todos los días durante un año en San Francisco. Se trata de una autentica matriz de 20 columnas y18 filas, que hacen los 360 días, pero hay que imaginarla en 3D, con un fondo de (calcular todo un día en segundos y dividirlo por 10.
Cada celda es la secuencia de todo un día.

Por supuesto se ve cuando es de noche, y si os fijáis, se ven los días que ha llovido, el tipo de Luna que podía haber,....,da para mucho juego este vídeo.

Visualizarlo en pantalla completa y con buena resolución.

Podéis visitar el "Post" a que hago referencia, donde da interesantes detalles de como fue realizado.

Lego Robots solving Rubik´s Cube

Descubrí de estos videos a traves de un tweet y de ahí conocí un magnifico blog:
http://blog.revolutionanalytics.com/
Os recomiendo visitarlo.

Distancia de Mahalanobis_review 005

En una de las primeros posts sobre "Distancia de Mahalanobis", vimos la formula del cálculo de la distancia entre dos puntos en el espacio de componentes principales. Podemos considerar esto aplicado a algunos softwares como la manera de calcular la distancia de una muestra respecto a las otras del grupo. En el caso de la muestra más cercana, se tratará de su vecino mas próximo. Win ISI expresa este valor como NH.

Sin embargo si queremos conocer la distancia entre una muestra y el centro de la población, una de las muestras (el espectro medio) tiene como valor cero y la fórmula vista en el gráfico de la entrada anteriormente comentada cambia.

Estos días surgió una pregunta sobre este tema en el NIR Forum y Pierre Dardenne, adjunto una hoja Excel, donde se muestra que este cálculo lo aplica Win ISI para el cálculo de la GH.

Volveremos sobre este tema, pues me interesa bastante y mi idea es tratar de representarlo en un próximo vídeo.

Unscrambler: PLS Regression (Part 3)

En Unscrambler podemos marcar las muestras anómalas y recalcular sin ellas. Hacemos esto sin las muestras que comentamos anteriormente.
Las cosas cambian, ahora solo dos términos son necesarios para explicar la mayoría de la varianza. se observan también agrupaciones en función del valor de número de octano.

 Se observan también agrupaciones en función del valor de número de octano.

Los estadísticos de validación "leverage" para la regresión son:

1º Cumpleaños de NIR-Quimiometría

Este 1 de Diciembre de 2011, se puede considerar como el primer cumpleaños de este Blog. Los resultados son bastante satisfactorios y por supuesto me animan a continuar este próximo 2012.
Aprovecho este comentario para saludar a todos los visitantes asiduos, de todos los países (España, U.S.A, toda América Latina, Europa, Rusia,.....).
Gracias a los "followers" (Blog, twitter, canal de youtube,....).
Estas son las visitas recibidas mas numerosas, que junto a otras completan las casi 10200 a día de hoy.

Unscrambler: PLS Regression (part 2)

Después de desarrollar la regresión PLS, debemos fijarnos en el gráfico de Varianza Explicada o Varianza residual (depende del que más nos guste). En el caso de la varianza explicada, lo normal es que aumente en función de los términos que vayamos añadiendo. No olvidemos que este cálculo lo realiza con el método de validación que hayamos elegido (leverage o cross validation). En este caso estamos usando leverage.

NASA: Lanzamiento de Curiosity

Increible y espectacular Misión de la NASA en Marte, esperemos que todo salga según los planes previstos que son realmente espectaculares.

Parece el trailer de una película de ciencia ficción, pero son los planes que tiene la NASA para el aterrizaje de Curiosity en Marte.

Otros videos interesantes:

Laboratorio donde se construyó Curiosity

Unscrambler: PLS Regression (Part 1)

Ya os he comentado la imprescindible ayuda que proporciona el libro "Multivariate Data Analysis - in practice" del Kim H. Esbensen para iniciarte en la práctica de Unscrambler. Lo hemos estado haciendo en la serie "Repasando Unscrambler" con datos espectroscópicos de espectros de gasolina.

Esta serie de espectros los estudia también A.M.C. Davies en la Tony Davies Column en tres artículos:

The value of pictures 10/4 (1998).

More pictures from PLS regression analysis 10/6 (1998).

Uncertainty testing in PLS regression 13/2 (2001).

Podéis encontrarlos y descargarlos en Spectroscopy Europe.

En ellos comenta la importancia de mirar a los gráficos que se generan y no simplemente a los ya conocidos X-Y plot, así como a estadísticos como el RSQ y SEP.

También comenta en estos artículos, un comentario de Ian Cowe, que realmente debemos de tener en cuenta "What we (chemometricians) do is mainly to look at the pictures". 

Es importante por tanto, para nosotros que tratamos de introducirnos y profundizar en lo posible en este complejo mundo de la quimiometría de interpretar y entender los gráficos que se generan con el proceso de calibración y no solo quedarnos con el resultado final.

Hemos estado trabajando con los espectros con los análisis PCA, y ahora lo haremos con la regresión  PLS1.

En la regresión se recomiendan usar 3 factores, por lo que podemos ver mapas de dos dimensiones:

Term 1 vs Term 2

Term 1 vs Term 3

Term 2 vs Term 3

Observemos el 1 vs 2:

Volvemos a encontrar las muestras M52 y H59, que son las dos muestras aditivadas.

Estas muestras en el gráfico de influencia (usando los tres términos)  y en el eje de varianza residual Y, muestran un valor practicamente de cero:

Teniendo la H59 una gran influencia sobre el modelo.

Sin quitar ninguna muestra y con los tres factores PLS, el gráfico X-Y  es:

Repasando Unscrambler - 006 (Sample Residuals)

En Unscrambler podemos ver los residuales espectrales para cada muestra a medida que se añaden PCs. No olvidemos que partimos de las muestra centrada.

Observemos (de izquierda a derecha y de arriba a abajo) los residuales espectrales a medida que se añaden PCs. El primer gráfico es de la muestra centrada, el 2º el residual con 1 PC, el 3º con 2 PCs, el 4º con 3 PCs (el recomendado por el modelo) y el 5º con 4 PCs (uno más del recomendado con lo que podiamos entrar en problemas de overfitting).

Win ISI 4.4 (New update available)

You can download a new version of Win ISI 4 (4.4) that fix the bugs reported in Win ISI 4.3

Os podéis descargar la nueva actualización de Win ISI 4 (la 4.4) que soluciona los problemas reportados en la versión 4.3.

http://www.winisi.com/

WinISI version 4.4.0.13316 Update

November 11, 2011

WinISI 4.4 update includes a new discriminate technique. The algorithm is maximum X-residual and it is fully supported in ISIscan version 4.4.

The maximum X-residual models are saved in files with the extension .DC5. This discriminate techique joins the original 2-block PLS, maximim distance, correlation, Mahalanobis distance, and X-residual methods for maximum flexibility in designing your discriminate analytical system.

WinISI 4.4 update also includes some bug fixes and minor enhancements.

WinISI 4.4 is available as a free upgrade to all licensed users of WinISI 4.

If you want to use the new discriminant method DC5, you need to download the ISI Scan 4.4 also in the Win ISI web page.

Dont forget to make a copy of the DATA folder or a Backup before to update, just in case there are any problems to come back to the previous version.

Repasando Unscrambler - 005 (X- Loadings)

Hemos visto en 001, los espectros y en que zonas había una mayor varianza, con los márgenes de desviación estándar y los cuartiles. Como sabemos al calcular los componentes principales,, calculamos los "loadings" (la ya varias veces comentada Matriz "P"). Estos Loadings son espectros que nos servirán para reconstruir otros espectros. Disponemos de tantos loadings como PCs, y en el ejemplo que estamos desarrollando en este repaso, la recomendación es de 3 PCs.

El primer PC, esta relacionado con la mayor fuente de varianza espectral, una vez extraida esta varianza, se calculan los demás extrayendo las demas fuentes de varianza,...
Observar estos Loadings requiere un cierto conocimiento de espectroscopía (donde están las bandas de los diferentes analitos, interferencias,.....).

Repasando Unscrambler - 004 (Residual X - Leverage)

Este gráfico es de gran importancia, a la hora de determinar si descartamos muestras como anómalas o las mantenemos. Algunas muestras tienen un alto residual y separan del resto de muestras, pero pueden hacerlo de distinta forma. Pongamos un simple ejemplo.

Una serie de muestras se describen perfectamente con dos componentes principales, que como sabemos describen un plano. Sus proyecciones sobre dicho plano serán mas o menos pequeñas en función de su residual X, pudiendo caer sobre el mismo plano, en cuyo caso su residual sería cero. En el caso de que alguna muestra, tenga un alto residual y su proyección sobre el plano sea muy grande, dicha muestra es un anómalo por alto residual y es muy probable que tengamos que descartar dicha muestra.

Por otra parte puede haber muestras con un residual, pequeño, pero que se aparta del resto de muestras considerablemente, esta muestra se considera de gran influencia en el modelo y tiene un gran peso al describir los componentes principales. En este caso debemos de considerar el mantenerla previo estudio de la muestra (¿pertenece a la misma población?, ¿es una muestra con una concentración de analito alta?,....).

Puede ocurrir el caso en que la muestra tenga un alto residual, así como una alta influencia.

Para el ejemplo que estamos viendo en la serie "repasando unscrambler", el gráfico "Residual X vs Leverage" es:

El gráfico de barras nos muestra los residuales de validación en rojo para cada una de las muestras. Claramente destacan los de las muestras M52 (penúltimo) y H59 (último).Vemos que la muestra H59, tiene un menor residual en el modelo final (azul), pero un alto residual en el de validación, pero esto tiene su lógica, porque hemos utilizado la validación cruzada (leave one out), y cuando esta muestra esta en el grupo de validación, no hay ninguna como ella en el de calibración y el residual de validación es muy alto.

Repasando Unscrambler - 003

Realizamos el análisis de Componentes Principales para una mejor comprensión de nuestra base de datos. Los gráficos de "varianza explicada" , nos indican que tres PCs son suficiente para explicar la variabilidad de nuestros espectros.

Repasando Unscrambler - 002

Una vez observados los datos de la matriz X (espectros), observaremos los de la matriz Y (valores de referencia), y para ello como ya hemos hecho en otras ocasiones la mejor opción es el histograma.

Repasando Unscrambler - 001

A lo largo de una serie de entradas, iré repasando conceptos de Unscrambler para datos espectroscópicos. Existe un maravilloso libro "Multivariate Data Analysis - in practice" del profesor Kim H. Esbensen que es una guía perfecta para repasar algunos conceptos y meterse posteriormente en mas profundidad con otra serie de datos.

Histogramas (Skewness - Kurtosis)

We have seen some of the statistics linked to the histograms, but these two (in this case given by Unscrambler) can be very usefull for a better understanding of our constituent database.

Skewness & Kurtosis

Wikipedia:
Skewness.....Asimetría
Kurtosis......Curtosis

Shoot-out 2008_parte 006

Al igual que en las entradas previas, desarrollo la calibración con el software VISION, los tratamientos usados anteriormente no dan tan buenos estadísticos y en esta ocasión funciona mejor el tratamiento de 2ª derivada, para los mismos segmentos espectrales.

Same as previous posts, I have developed the calibration with another software (VISION), here the same math treatment an wavelengths regions as in the others, does not give the same statistics (a little bit worse), but the the 2º derivative gives a SEP similar.

Estadísticos de calibración / Calibration Statistics:

Para no tener overfitting VISION utiliza el estadístico PRESS, del que hablaremos proximamente:

To avoid overfitting VISION use the PRESS Statistic (We will talk about it soon)

Validamos con el conjunto de validación de la Campaña del 99, obteniendo:

Validation with the validation set.

El error de predicción SEP es de 0,1799.

The Standard Error of Prediction is: SEP = 0,1799

Visión nos dá los de Bias Pendiente e Intercepto y nos dice que en caso de ajuste el SEP bajaría a 0,1626. No obstante esto se debe ignorar.

Proximamente probaremos con Matlab y Unscrambrer para dar una evaluación general de los estadísticos de este parámetro.

Shoot-out 2008_parte 005

En Shoot-out 2008_parte 004 usamos una ecuación PLS, vamos a probar que pasa con las LOCAL. ¿Mejorará la predicción?.
In Shoot-out 2008_parte 004 we used PLS to develop the equation, now we are to deveop the equation with LOCAL. Will it improve the predictions?.
Minimun number of samples: We can use 75.
Maximun number of samples: We will use Batch Mode (100, 150, 200, 250, 300 and 350).

SEP values are quite similar with 200, 250, 300 and 350.
We can select 200 for our LOCAL model.
Now we have to find the best configuration for "minimun & Máximun numder of factors". Wé will check all along the allowed values (minimun 1, maximun 50):

The best combination found was: Min = 5, Max = 27

We used  SNV-Detrend 1-4-4-1 as Math treatment which it seems to work quite well for this product.

For some reasons (can be explained in a near future if comment are added) when put it into routine statistics change a little bit, and this are the values that we will compare with the other models.

Shoot-out 2008_parte 004

Desarrollando la ecuación (para proteína).
Developing the equation (for protein).

Modified PLS Regression Statistics    

Input File……………………………………   FRED2008.CAL 

Validation File…………………………….  fred99a.cal           

Math Treatment ……………………….  1, 4, 4, 1            

Number of variables…………………..  768

Scatter Corr. …………………………….   SNV and Detrend       

Downweight outliers………………….  No

Constituent ……………………………....  WHTPRO                 

Number of samples…………………….  774

Mean    ………………………………………..13.670              

 Range………………………………………….10.00 - 17.00     

Std Dev……………………………………….. 1.367

 

CALIBRACIÓN					VALIDACIÓN
Terms	SEC	RSQ	SECV	1-VR	SEV	BIAS	SEV(C)
15	0.160	0.986	0.180	0.983	0.179	0.038	0.176

 

El RPD para la validación es:

RPD = 1,536 : 0,179 = 8.58

Shoot-out 2008_parte 003

Se han actualizado las entradas previas de Shoot-out 2008 (001 y 002) con nueva documentación.

El objetivo del Shoot-out 2008 era desarrollar la mejor calibración posible para diferentes parámetros, entre ellos uno de los que mejores resultados proporciona para la técnica NIR, la proteína, pero también de otros parámetros de tipo físico y reológico.

Para validar la ecuación, se dispone de un conjunto independiente, pues se han dejado los resultados de una campaña fuera (la de 1999).

Iremos incluyendo diferentes entradas sobre este Shoot-out 2008, a modo de ejercicio para ver los diferentes métodos de calibración (globales, locales, redes neuronales,...,etc). y con diferentes software (Win ISI, Vision, Matlab, Unscrambler,...).

Como es lógico realizamos un análisis de PCAs, para comprobar la existencia de anómalos, grupos,...Debido a los problemas que hemos visto en las entradas anteriores, y también a la variedad de clases de trigo, y otras fuentes de varianza, el programa selecciona un número elevado de componentes principales y determina que la muestra 70, es anómala. Si observamos las proyecciones de las muestras sobre los componentes principales, podemos determinar el que componente la muestra es anómala.

Sobre el PC 23.
La muestra se va respecto al límite de desviación estándar fijado.

Se pueden probar diferentes tratamientos matemáticos, para ver si la "muestra 70" no sale como anómala, pero en los probados siempre sale y con un valor bastante alto, por lo que se decide excluirla de la calibración.

Tweet

Cálculo de los Eigenvectors / Eigenvectors Calculation

Continuamos con el ejercicio de la entrada anterior (donde calculamos los eigenvalues), calculando ahora los eigenvectors.
Entrada anterior: Cálculo de los Eigenvalues
Now we calculate the eigenvectors once we know (from the previous post) the eigenvalues.
Previous post: Eigenvalues Calculation