library(tidyverse)
library(prospectr)
load("C:/BLOG/Workspaces/NIR Soil Tutorial/post5.RData")R & Chemometrics
R for Statistics and Near Infrared spectroscopy
27 jun 2025
19 jun 2025
17 jun 2025
Standard Normal Variate (SNV)
As in previous posts, we are going to follow the Soil spectroscopy training material and we are going to use the reference material provided.
Let´s start loading the libraries and the data:
In the training material we can read a clear explanation of what SNV does:
“Standard normal variate is a simple and widely used method that works by centering each individual spectrum to zero and then dividing each spectral band value by the standard deviation of the entire spectrum. The SNV method processes each observation independently. The disadvantage of SNV is that it can be sensitive to noise”.
So for each spectrum we calculate the mean of all data points reflectance values and also their standard deviation. Then we subtract for every data point the mean and divide the result by the standard deviation.
Using the prospectr package, we can use the standardNormalVariate function to apply the SNV transformation to the spectra matrix.
Let´s use first classical R function matplot to plot the spectra before and after the SNV transformation:
matplot(colnames(dat$spc),
t(snv_spectra),
type = "l",
col = "grey",
lwd = 0.5,
xlab = "Wavelength (nm)",
ylab = "Reflectance",
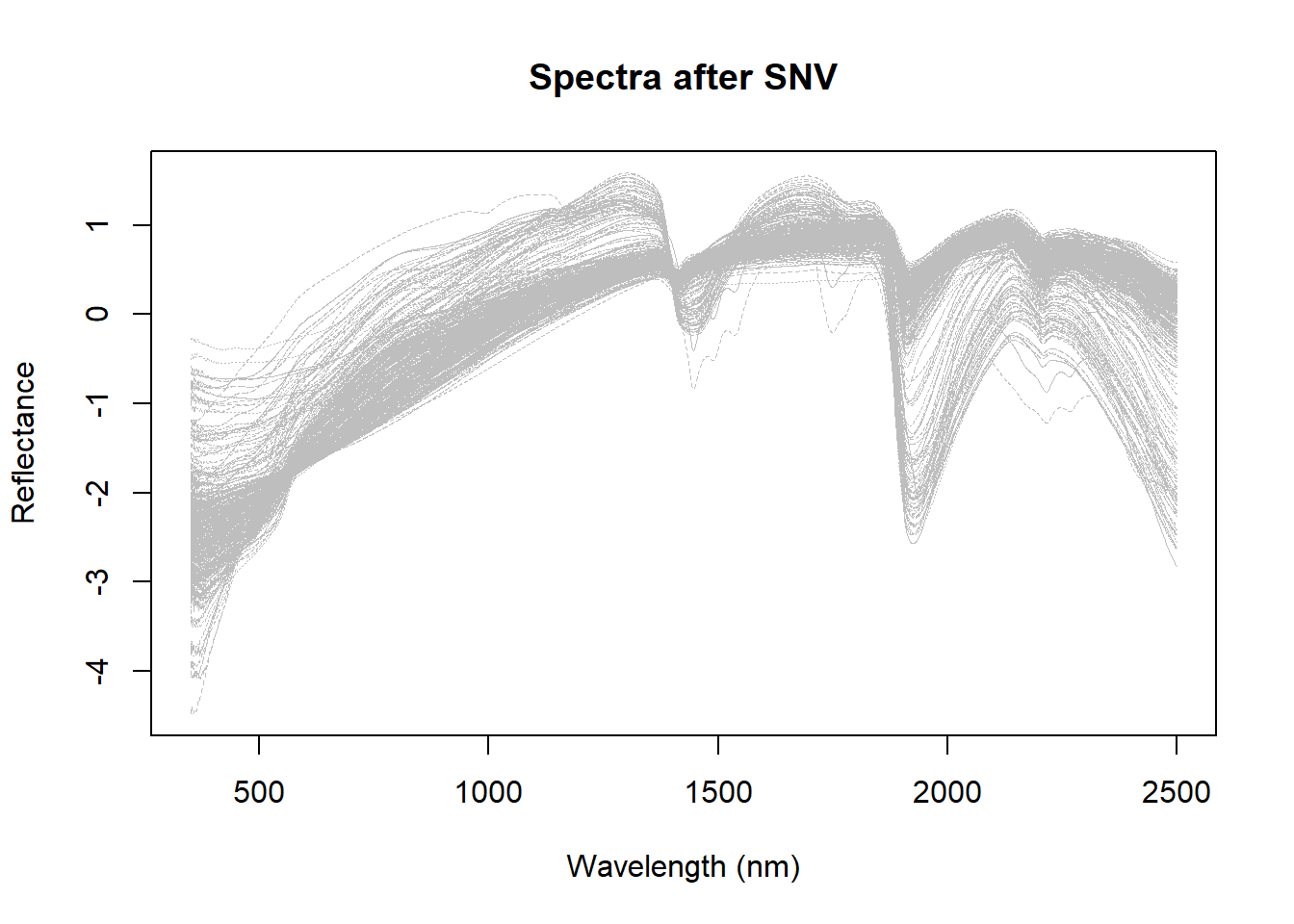
main = "Spectra after SNV"
)
Now with ggplot2:
# Create the long-format data frame for the different derivatives
snv_spectra_long <- data.frame(
sample = rep(1:nrow(dat), each = ncol(snv_spectra)),
oc = rep(dat$Organic_Carbon, each = ncol(snv_spectra)),
clay = rep(dat$Clay, each = ncol(snv_spectra)),
silt = rep(dat$Silt, each = ncol(snv_spectra)),
sand = rep(dat$Sand, each = ncol(snv_spectra)),
wavelength = rep(my_wavelengths, nrow(snv_spectra)),
absorbance = as.vector(t(snv_spectra))
)
ggplot(snv_spectra_long, aes(x = wavelength, y = absorbance,
group = sample, color = oc)) +
geom_line(alpha = 0.5) + # Set alpha to 0.5 for transparency
scale_color_gradient(low = 'blue', high = 'red') +
theme_minimal() +
labs(x = 'Wavelength (nm)', y = 'Reflectance', color = 'Organic Carbon (%)')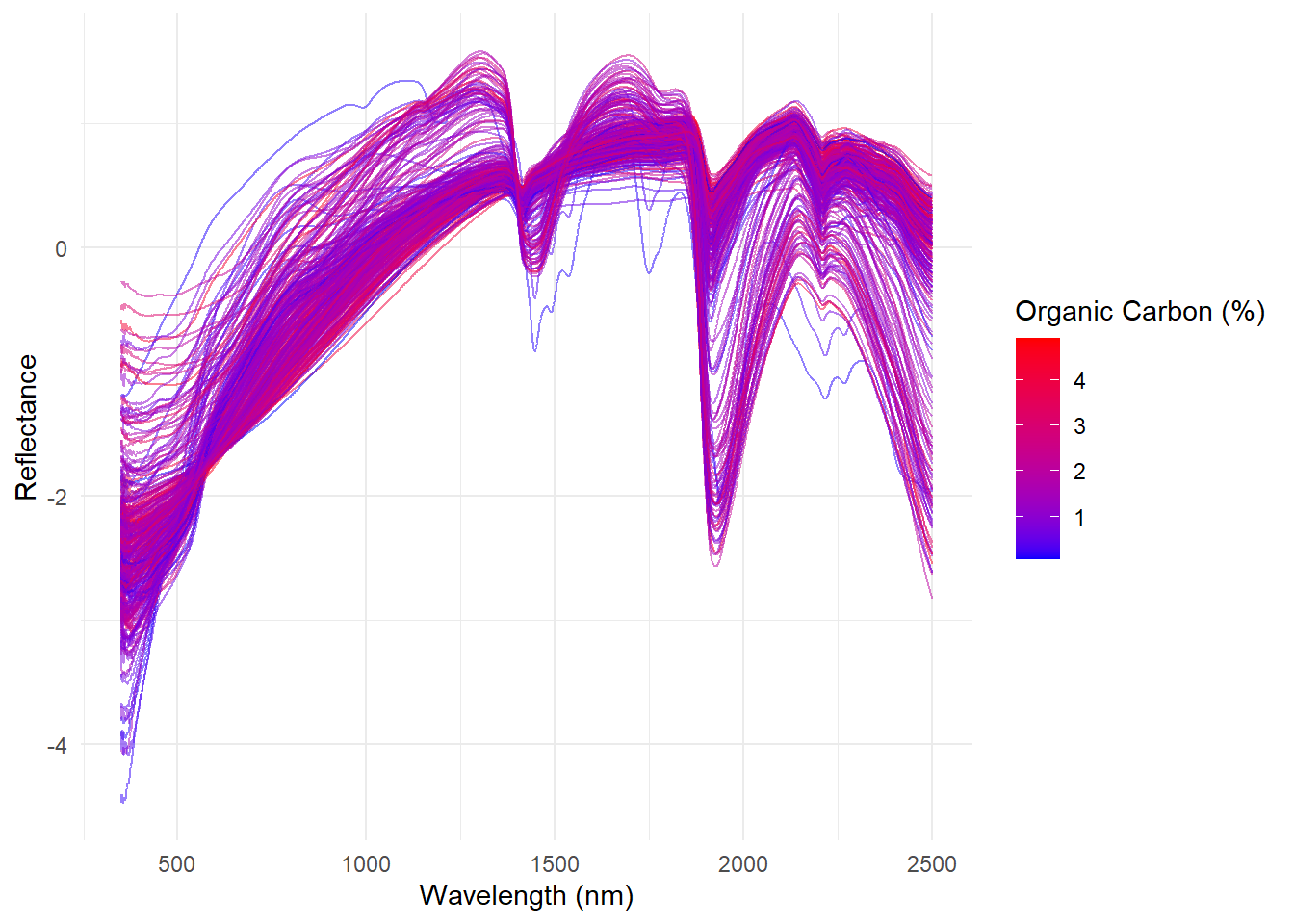
Bibliography:
Soil spectroscopy training material Wadoux, A., Ramirez-Lopez, L., Ge, Y., Barra, I. & Peng, Y. 2025. A course on applied data analytics for soil analysis with infrared spectroscopy – Soil spectroscopy training manual 2. Rome, FAO.