PCR vs. PLS (part 2)

Continue from post: "PCR vs PLS (part 1)":

As we add more terms to the model (PCR or PLS) the Standard Error of Calibration decrease and decrease, for this reason is necessary to have a validation method to decide how many terms to keep.

Cross Validation, or an External Validation set are some of the options to use.

The "PLS" R package has the function "RMSEP" which give us the standard error of the calibration, and we can have an idea of which terms are important for the calibration.

Continuing with the post PCR vs PLS (part 1), one we have the model we can check the Standard Error of Calibration with the 5 terms used in the model.

RMSEP(Xodd_pcr, estimate="train")
(Intercept)      1 comps      2 comps      3 comps      4 comps      5 comps  
      1.985        1.946        1.827        1.783        1.167        1.120 

 

As we can see the error decrease all time, so we can be tempted to use 5 or even more terms in the model.

One of the values of the  pcr function is "fitted.values" which is an array with the predictions depending of the number of terms.

As we can see in the RMSEP values, 4 seems to be a good number to choose, because there is a big jump in the RMSEP from R PC term 3 to PC term 4 (1.783 to 1.167), so we can keep the predicted values with this number of terms and compare it with the reference values to calculate other statistics.

 

Anyway these statistics must be considered as optimistic and we have to wait for the validation statistics (50% of the samples in the even position taken apart in the post "Splitting Samples into a Calibration and a Validation sets" .

Statistics with the Odd samples (the ones used to develop the calibration)
pred_pcr_tr<-Xodd_pcr2$fitted.values[,,4]
##The reference values are:
ref_pcr_tr<-Prot[odd,]
## We create a table with the sample number,
## reference and predicted values
pred_vs_ref_tr<-cbind(Sample[odd,],ref_pcr_tr,pred_pcr_tr)

Now using the Monitor function I have developed:
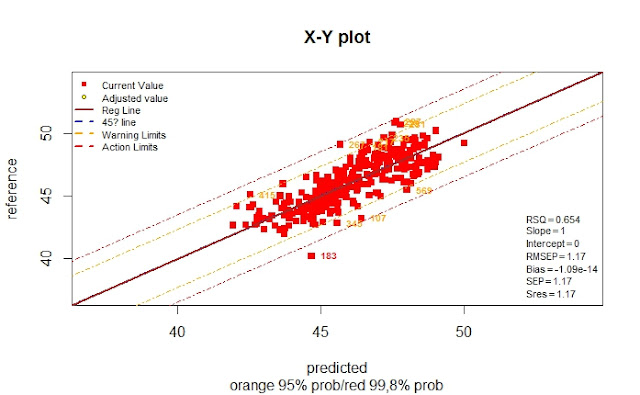
monitor10c24xyplot(pred_vs_ref_tr)

We can see other statistics as the RSQ ,Bias,...,etc.

Now we make the evaluation with the "Even" samples taken apart for the validation:

library(pls)
pred_pcr_val<-as.numeric(predict(Xodd_pcr2,ncomp=4,newdata=X_msc_val))
pred_pcr_val<-round(pred_pcr_val,2)
pred_vs_ref_val<-data.frame(Sample=I(Sample[even]),
                 Reference=I(Prot_val),
                 Prediction=I(pred_pcr_val))
pred_vs_ref_val[is.na(pred_vs_ref_val)] <- 0  
                 #change NA by 0 for Monitor function

As we can see in this case the RMSEP is a Validation statistic, so it can be considered as the Standard Error of Validation, and its value it´s almost the same as the RMSEP for Calibration.

RMSEP Calibration .........1,17

RMSEP for Validation .....1,13