Validating R-PLS Sunflower Seed Model (Part 01)

I have ten new sunflower seed samples, with laboratory data and I´m going to use them to validate the performance of a model developed in R with PLS:
Sunflower seed Regressions with "R" - 001

First, I  have a look to the spectra of the validation set (red spectra) compares with the training spectra (blue spectra), without any math treatment applied:

and after, with the MSC applied:

I see clearly some differences, but the idea is to check if the calibration is robust enough to predict the samples according to the statistics we got in the summary of the regression.
In the summary of Sunflower seed Regressions with "R" - 001 , we decide to use 7 terms for our predictions, so:

predict(sflw.g00rmn,ncomp=4,newdata=sflw.msc2.val)

                     G00rmn
171     46.25923
173     53.07202
176     53.48508
177     53.27027
178     46.05511
179     46.73826
180     50.95862
181     52.44956
182     47.59493
183     46.51557
The error is:

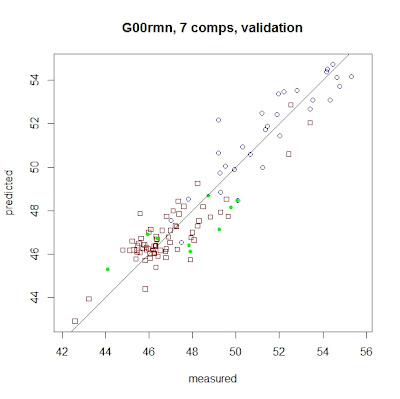
Let´s have a look to the "Reference vs Predicted" plot:

predplot(sflw.g00rmn,ncomp=7,newdata=sflw.msc3.val,
asp=1,line=TRUE,col=c("red"))

 

Transfering "oil / fat" Database - Transflectance

Today I have the task to transfer a oil/fat database from one instrument to other three instruments. Three of them are the same type and the other (where the database come from) has a different sample presentation (aluminum reflector), but all of them has the same sample presentation mode: "Transflectance".

 It is important to present the samples in the instruments at the same temperature.

Be careful that the sample covers the reflector without bubbles or gaps.

The gold reflectors are 0.1 mm, so the total path length is 0.2 mm. Anyway we must be careful because there are some minimum differences between them, and every instrument must use their respective reflector for the standardization.

These are the spectra of water acquired in the same instrument, but with three different gold reflectors of 0,1 mm.

 

LOCAL: Batch Mode to select Max Number of Samples

When working with LOCAL we have the choice to select the “Minimum Number of Samples” and the “Maximum Number of Samples” to develop the LOCAL calibration. This option can be done with the default option (where we can select the maximum and minimum values), or with the Batch mode where we select the Minimum and create a Batch for the Maximum (in this case 200, 250 and 300). We leave the software running this task and at the end we will get some statistics (SEP, RSQ, Bias…) and the Rank for the best choice for the “Maximum Number of Samples”.

I use a sample set with to check the best option with 213 values for moisture (HD), 238 for ash (CZ), 242 for fat (GB) and 235 for protein (PB).

The DataBase used is PetFood and in the validation set there was sample of different kinds of dogs and cats.

In this example the Best Choice is 300 samples so we can configure the Batch for more samples, just in case we get better statistics.

 

 

This is the Lab vs. Predicted plot (for the Validation Set), in the case of Fat (GB) selecting a maximun of 300 samples.

Access to Statistics: The top 20 data visualisation tools

Access to Statistics: The top 20 data visualisation tools: The top 20 data visualisation tools | .net magazine 17th Sep 2012 | 09:17 From simple charts to complex maps and infographics, Brian S...

Reference Standardization Concept

Vision has an option to import DA files (from NSAS ) into a project, so we import the file which comes with our standard set and we will see one file called R80xxxxx (the “x” are the serial number of the standards box set). This file is our Master Reference file.

If we acquire the spectra of this R80xxxxx in the Host instrument (our instrument), without reference standardization , the spectra is quite different to the Master spectra, so a Reference standardization is needed in order that the Master and the Host have in common the same reference spectra when acquiring a sample.

 

In the next picture we see the spectra of the R80xxxxx (Red in the Master and Blue in the Host without Ref STD).

 

We run the Reference standardization and a STD file is created to correct this differences from the Host to the Master. Other Hosts do the same and the idea of more transferable equations (between instruments) is possible because we are correcting most of the instruments differences.

Here we are not correcting wavelength shift, just photometric response.

There are standards sets with different ceramics in order to check the photometric response of the Host to the Master at different reflectance levels (R99xxxxx, R40xxxxx, R20xxxxx, R10xxxxx and R02xxxxx).

 

Let´s compare the R99xxxxx passed in the Host instrument with and without Reference Std.

 

Without Ref Std:





 

With Ref Std:

 

 

 

 

Sunflower seed Regressions with "R" - 001

I have spectra from sunflower seed grinded from 3 NIR instruments (range 400-2500 nm). I prepare the data frame separating the spectral range in two segments (Segment 1 or VIS from 400-1100 nm, and segment 2 or NIR from 1100 to 2500). Reference values are from four different laboratories.
 

In a previous post I have transformed the NIR raw spectra to MSC, using a function from the R package "Chemometrics with R".
 

In this post I want to run a regression with PLS (PLSR) using the Segment 2, and with the math treatment MSC.

sflw1 <- plsr(G00rmn~NIRmsc, ncomp = 10,data =sflw.msc2 ,
        validation = "LOO")

VALIDATION: RMSEP
Cross-validated using 107 leave-one-out segments.
      
          (Intercept)  1 comps  2 comps  3 comps   4 comps   5 comps  6 comps

CV           2.87         2.465       2.074      1.112      1.038     0.9903     0.9833
adjCV      2.87         2.465       2.074      1.111      1.038     0.9899     0.9829

                         7 comps  8 comps  9 comps  10 comps
CV                     0.9746     0.9781    0.9754    0.9683
adjCV                0.9741     0.9775    0.9745    0.9675


 TRAINING: % variance explained

              1 comps  2 comps  3 comps  4 comps  5 comps  6 comps  7 comps  8 comps
X              41.93     89.86       95.78      97.02      98.21      99.21      99.62      99.76
G00rmn    31.47     51.80       86.47      89.14      90.36      90.64      91.01      91.42

              9 comps  10 comps
X              99.81     99.89
G00rmn    92.30     92.62

 

And now we can see the X-Y plot for the LOO Regression (with 7 comps), with different colors and symbols for the samples from the different instruments.

plot(sflw1, ncomp = 7, asp = 1, line = TRUE,

pch=c(20:22)[sflw.msc2$Operator],
col=c("green","blue","brown")[sflw.msc2$Operator])