Tidyverse and Chemometrics: The power of graphics (part1)

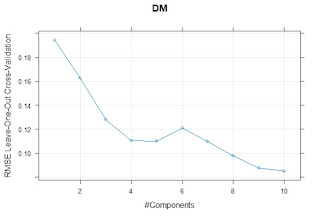
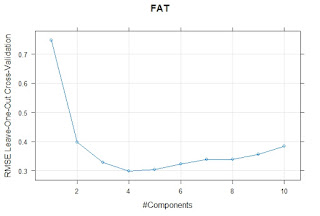
I have a dataset with values for different types of Iberian ham of different qualities analyzed by the reference methods and by a Near Infrared Transmission Method.  We are using for the prediction a Meat Calibration Model where probably this type of samples are not represented so some adjustments can be necessary, and we want to check if its better to do it in general or individually by types of ham.

 

We have data for moisture, protein, fat, salt and water activity. This data is not cleaned, so we will have to remove probably some samples due to a wrong lab values or samples not well presented to the instrument due to several reasons.

 

We can start by Moisture in this post, and we can plot on the X axis the Predicted Value and on the Y axis the lab Value. We use colors to see in a better way how the samples fit in the plot and from the plot we can take conclusions about which types of products have less or more water.

ggplot(ham_data,aes(x = Moi_FSC, y= Moi_LAB,color = Product)) +
                    geom_point()

Let´s look to the data by product, so we can have a better knowledge about every product:

ggplot(jamon_data,aes(x = Moi_FSC, y= Moi_LAB,color = Product)) +
                      geom_point() +
                      facet_wrap(~Product)

If we have all this information in plots for the different constituents and product we can make a visual understanding of every product. We can check apart the statistics later , but it is clear that the impact of the tydyverse plots is great.

Tidyverse and Chemometrics (part 17): Selecting samples for monitoring

Now we can select the samples manually from the scores maps using the identify funtion, so we vcan enlarge the maps and select the samples we consider that cupture the structure of the new population and at the same time expand the calibration.

These are  the views for the samples wher the blue ones are the samples from the seasons 1 and 2, the ones used for the calculation of the principal components. The red ones and green ones are the projected samples of Fish3 season, beeing the red ones the selected ones to send to the laboratory for the calculation of "dry matter", "protein", "fat" and "ash".

Now we process these selected sample by the model to get the predictions.

library(caret)
fish3_caret_prot_pred<-predict(model_fish12_prot_pls,
                               ncomp=10,
                               newdata =fish3_sel_df )
fish3_caret_dm_pred<-predict(model_fish12_dm_pls,ç
                             ncomp=10,
                             newdata =fish3_sel_df )
fish3_caret_fat_pred<-predict(model_fish12_fat_pls,
                              ncomp=4,
                              newdata =fish3_sel_df )
fish3_caret_ash_pred<-predict(model_fish12_ash_pls,
                              ncomp=10,
                              newdata =fish3_sel_df ) 

Ans finally we create a dataframe with the predicted and reference values to check the performance of the predictions. 

> fish3_selected_monitor
   Sample Month Year    DM PROTEIN   FAT   ASH DM_PRED PROT_PRED FAT_PRED ASH_PRED
7     7F2    12 1991 93.57   70.90 10.66 18.34   93.95     71.93     9.67    16.68
8     8F2    12 1991 94.25      NA    NA    NA   94.56     75.94    10.22    13.13
9     9F2    12 1991 94.01   75.05  9.83 14.90   94.41     75.74     9.19    14.03
11   11F2    12 1991 93.60   75.35 11.53 12.91   93.84     77.20    10.89    11.17
12   12F2    12 1991 93.68   71.14 11.50 16.93   93.97     72.40    10.87    15.98
13   13F2    12 1991 93.44   70.15 10.77 17.16   93.67     72.21    10.29    16.06
16   16F2    12 1991 92.89   70.70 12.22 16.86   93.25     71.27    11.14    16.66
17   17F2    12 1991 94.66   71.71 10.94 16.72   94.73     74.51    10.34    15.38
18   18F2    12 1991 93.27   72.81 10.49 16.06   93.44     74.84     9.60    14.82
23   23F2    12 1991 93.96   73.76 10.37 15.45   94.39     74.62    10.23    15.47
27   27F2    12 1991 93.41   66.88  9.37 22.79   93.84     66.99     8.05    22.22
28   28F2    12 1991 94.11   77.25 11.96 10.16   94.34     78.92    11.54    10.18
29   29F2    12 1991 93.16   68.53 11.28 20.09   93.76     70.97    10.27    18.75
33   33F2    12 1991 94.33   78.06 11.50 10.86   94.72     78.70    11.63    10.55
34   34F2    12 1991 93.72   65.04  9.35 25.08   94.08     66.04     8.40    23.49
36   36F2    12 1991 94.18   64.49  9.17 26.03   94.57     64.41     8.16    25.56
38   38F2    12 1991 92.65   63.69 10.24 25.11   93.10     64.09     8.88    24.41

  

Tidyverse and Chemometrics (part 16): Projecting a new season

We have developed the calibration for fish meal with Fish1+2 seasons (see previous post) and meanwhile we have new spectra for samples (47) from a new season (Fish3) that we acquire on the NIR instrument. These samples are processed by the model and give some results, and one of the questions could be: how accurate are those results?.

Send the 47 samples to the lab will be too costly, so we want to send a set of samples, which captures the structure of the new fish3 samples, and at the same time add new variability to the actual database. Doing this, the next time we create a new calibration it will be more representative for the fish meal population, hopping to get better accuracy for the fish4 set and so on.

The idea this time, is to make it in a manual way, projecting the samples and selecting a certain number based on the money we want to expend in laboratory analisis.

We have seen the calculation for the projections in a previous post, so we just draw the new season scores (in red) over the PC space of the previous seasons 1 and 2, showing the scores for fish1 and fish 2 in blue color.

#PC1 vs PC2
drawMahal2(fish_1d_all_pc$T[,c(1,2)],
          center=apply(fish_1d_all_pc$T[,c(1,2)],2,mean),
          covariance=cov(fish_1d_all_pc$T[,c(1,2)]),
          quantile=0.975,xlab="PC1",ylab="PC2",col="blue",
          main="Fish3 projected on Fish1+2 PCs")
par(new=TRUE)
drawMahal2(fish3_1d_T[,c(1,2)],
          center=apply(fish_1d_all_pc$T[,c(1,2)],2,mean),
          covariance=cov(fish_1d_all_pc$T[,c(1,2)]),
          quantile=0.975,xlab="PC1",ylab="PC2",col="red")

 We notice that many of the Fish3 samples are outside of the ellipse formed by Fish1 + Fish2 samples. We can check the other score maps:

The score maps show clearly that many of the samples are outliers.
We can calculate the Mahalanobis distance for every sample to check how many are outside the cutoff limits:

fish1y2_T_mean<-colMeans(fish_1d_all_pc$T)
fish3_d_mahal<-sqrt(mahalanobis(fish3_1d_T[,c(1:5)],
                    fish1y2_T_mean[c(1:5)],
                    cov(fish_1d_all_pc$T[,c(1:5)])))

     1F3      2F3      3F3      4F3      5F3      6F3 
1.808546 2.410371 1.817420 2.674472 3.882431 8.894017 
     7F3      8F3      9F3     10F3     11F3     12F3 
3.956726 4.129471 4.194344 4.608712 5.637123 4.561250 
    13F3     14F3     15F3     16F3     17F3     18F3 
5.020347 3.427444 3.330089 3.348741 4.039378 4.006860 
    19F3     20F3     21F3     22F3     23F3     24F3 
7.992560 8.237418 5.813657 5.672932 6.258595 5.949936 
    25F3     26F3     27F3     28F3     29F3     30F3 
5.763188 6.121845 7.013205 6.370521 6.109572 3.944506 
    31F3     32F3     33F3     34F3     35F3     36F3 
2.576640 2.675160 3.993163 6.187790 7.092179 7.118996 
    37F3     38F3     39F3     40F3     41F3     42F3 
3.460574 4.061820 4.202667 2.000492 1.806180 3.880191 
    43F3     44F3     45F3     46F3     47F3 
3.871592 4.937029 3.415351 4.433763 8.009396 

Without any doubt there are samples in these sample will expand the database but we have to capture the structure of this variability, removing samples that could be neighbours.

We proceed with this option in the next post. 

Tidyverse and Chemometrics (part 15): Updating the calibrations

Now that we have extended the database, it is time to develop a new calibration with the 57 fish meal samples (merge of fish1 and fish2). I use this time Caret package to develop the new regressions for protein, moisture , fat and ash.

Let´s start by protein, where we still maintain the leave one out cross validation for the selection of the number of terms and for the stimation of the error we can get for new samples.

model_fish12_prot_pls <- train(PROTEIN~nir_1d,data=fish_1d_all,
                         method = "pls",scale=FALSE,

                         na.action=na.omit,
                         trControl =trainControl("LOOCV"),
                         tuneLength = 10)

Now we can check the plot for RMSECV to see the number of terms necessary for the better stimation for the Cross Validation Error.

ggplot(model_fish12_prot_pls) 

 As we can see we get the best tune with 10 terms, but the error with 4 terms is almost similar.

We can try checking other type of cross validation using 10 groups (folds) for example, but we get similar results. It seems that the necessary number of terms will be of that order and we need to add more samples to make the protein calibration more robust and stable.

 
model_fish12_prot_pls <- train(PROTEIN~nir_1d,
                         data=fish_1d_all,
                         method = "pls",scale=FALSE,
                         na.action=na.omit,
                         trControl =trainControl( 
                         method = "cv",number=10),
                         tuneLength = 10)
We can see the statistics for every fold:

RMSE <dbl>	Rsquared <dbl>	MAE <dbl>	Resample <chr>
0.5201864	0.9423407	0.4304066	Fold02
0.5848165	0.9759022	0.4157110	Fold01
0.3711634	0.9824319	0.3066366	Fold05
0.5152365	0.9882782	0.4323673	Fold06
0.8049838	0.9051394	0.6675988	Fold10
0.6778746	0.8825006	0.5729103	Fold04
0.6068664	0.8418642	0.5406835	Fold08
0.8391941	0.9947530	0.6664207	Fold09
0.5109232	0.9887235	0.3951494	Fold03
0.5441377	0.9800517	0.4993318	Fold07

As we can see we have good correlations for every fold, and the RMSE (Root Mean Square Errors ) are  aceptable taking in account that the parameter is protein and we have not too many samples yet.

To get the final statistics we can use:

 getTrainPerf(model_fish12_prot_pls)

TrainRMSE <dbl>	TrainRsquared <dbl>	TrainMAE <dbl>	method <chr>
0.5975383	0.9481985	0.4927216	pls

 Where:

TrainRMSE..........Root Mean Square Error for the training samples
TrainRsquared.... R squared for the training samples
TrainMAE............Mean Absolute Error for the training samples

We can see in the following plots the terms for "Dry Matter", "Fat" and "Ash":

 In the next post we will get spectra from a new season and we continue in a different way selecting samples for the lab.